Algèbre
L’algèbre est la branche des mathématiques qui étudie les structures algébriques, indépendamment de la notion de limite (rattachée à l’analyse) et de la notion de représentation graphique (rattachée à la géométrie).
L’étude des structures algébriques peut être faite de manière unifiée dans la cadre de l’algèbre universelle.
Histoire
Antiquité
Les Babyloniens savaient déjà résoudre l’équation du 2e degré (ou équation quadratique).
Le premier document connu énonçant un problème algébrique tel que nous le connaissons est le Papyrus Rhind. Ce papyrus, actuellement (2007) au British Museum de Londres, date de -1650, ère chrétienne. Il comporte l’énoncé suivant :
- On doit diviser 100 miches de pain entre dix hommes comprenant un navigateur, un contremaître et un gardien, tous trois recevant double part. Que faut-il donner à chacun ?
Diophante, au IVe siècle, développe la méthode de résolution en nombres rationnels et découvre que le discriminant doit être le carré d’un nombre rationnel.
Perse et monde musulman

Page d’Algebra d’al-Khwarizmi
Le mot « algèbre » vient de l’arabe al-jabr (الجبر), qui est devenu algebra en latin et qui signifie « la réunion » (des morceaux), « la reconstruction » ou « la connexion » (en espagnol le mot algebrista désigne celui qui pratique le calcul algébrique mais aussi le rebouteux, celui qui sait réduire les fractures osseuses[1]).
C’est un des premiers mots de titre en arabe d’un ouvrage du mathématicien perse Al-Khawarizmi qui reprend, dans la première partie du IXe siècle, les travaux de Diophante d’Alexandrie (IVe siècle). Ce dernier avait imaginé de représenter une inconnue par un symbole nommé arithme. Le titre de cet ouvrage (Al-jabr wa’l-muqabalah) qui s’inscrivait dans l’époque d’essor des sciences et techniques islamiques (la culture de l’époque voulait que tout savoir soit traduit en arabe et disséminé dans tout l’Empire), a donné le mot moderne « algèbre ».
Après un voyage dans le nord de l’Afrique, Léonard de Pise dit Fibonacci fut séduit par cette nouvelle façon d’écrire les chiffres (différente des chiffres romains) et par le système décimal. Dès son retour au pays, il est parmi les premiers à populariser les chiffres arabes et le système décimal en Europe et travaille sur sa fameuse suite.
XVIe siècle : Europe
Le pape Gerbert d’Aurillac avait ramené d’Espagne vers l’an 1000 le zéro, invention indienne que les mathématiciens Al-Khawarizmi et Abu Kamil avaient eux-mêmes fait connaître dans tout l’Empire, et aussi à Cordoue.
Cette numération de position lance une ère de calcul algébrique, d’abord au moyen des algorismes nommés ainsi en hommage à Al-Kawarizmi, qui remplacent peu à peu l’usage de l’abaque. Les mathématiciens italiens du XVIe siècle (del Ferro, Tartaglia et Cardan) résolvent l’équation du 3e degré (ou équation cubique). Ferrari, élève de Cardan, résout l’équation du 4e degré (ou équation quartique), et la méthode est perfectionnée par Bombelli. À la fin du siècle, le Français Viète découvre que les fonctions symétriques des racines sont liées aux coefficients de l’équation polynomiale.
Jusqu’au XVIIe siècle, l’algèbre peut être globalement caractérisée comme la suite ou le début des équations et comme une extension de l’arithmétique ; elle consiste principalement en l’étude de la résolution des équations algébriques, et la codification progressive des opérations symboliques permettant cette résolution. À noter que c’est au français François Viète (1540-1603) que l’on doit l’idée de noter les inconnues à l’aide de lettres .
Au XVIIe siècle, les mathématiciens utilisent progressivement des nombres « fictifs », tels que l’une des racines carrées de -1, pour parvenir à calculer les racines non réelles de leurs équations. Cette « extension » des nombres réels (qui prendra le nom de nombres complexes) amène d’Alembert (en 1746) et Gauss (en 1799) à énoncer et démontrer le théorème fondamental de l’algèbre (ou théorème de d’Alembert-Gauss) : toute équation polynomiale de degré n en nombres complexes a exactement n racines (en comptant chacune avec son éventuelle multiplicité). Ou, sous sa forme moderne : le corps  des nombres complexes muni de l’addition et de la multiplication est algébriquement clos. des nombres complexes muni de l’addition et de la multiplication est algébriquement clos.
Le XIXe siècle s’intéresse désormais à la calculabilité des racines, et en particulier à la possibilité de les exprimer par des formules générales à base de radicaux. Les échecs concernant les équations de degré 5 amènent le mathématicien Abel (après Vandermonde, Lagrange et Gauss) à approfondir les transformations sur l’ensemble des racines d’une équation. Évariste Galois (1811 – 1832), dans un mémoire fulgurant, introduit pour la première fois la notion de groupe (en étudiant le groupe des permutations des racines d’une équation polynomiale) et aboutit à l’impossibilité de la résolution par radicaux pour les équations de degré supérieur ou égal à 5.
Une étape décisive était franchie avec l’écriture des exposants fractionnaires. Celle-ci permettra à Euler d’énoncer sa célèbre formule eiπ = − 1.
Algèbre moderne
Dès lors, l’algèbre moderne entame un parcours fécond : Boole crée l’algèbre qui porte son nom, Hamilton invente les quaternions, et les mathématiciens anglais Cayley, Hamilton et Sylvester étudient les structures de matrices. L’algèbre linéaire, longtemps restreinte à la résolution de systèmes d’équations linéaires à 2 ou 3 inconnues, prend son essor avec le théorème de Cayley-Hamilton (« Toute matrice carrée à coefficients dans 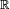 ou ou  divise son polynôme caractéristique »). S’ensuivent les transformations par changement de base, la diagonalisation et la trigonalisation des matrices, et les méthodes de calcul qui nourriront, au XXe siècle, la programmation des ordinateurs. Parallèlement, Kummer généralise les structures galoisiennes et étudie les structures de corps et d’anneau. Dedekind définit les idéaux (déjà entrevus par Gauss) qui permettront de généraliser et reformuler les grands théorèmes d’arithmétique. L’algèbre linéaire se généralise en algèbre multilinéaire et algèbre tensorielle. divise son polynôme caractéristique »). S’ensuivent les transformations par changement de base, la diagonalisation et la trigonalisation des matrices, et les méthodes de calcul qui nourriront, au XXe siècle, la programmation des ordinateurs. Parallèlement, Kummer généralise les structures galoisiennes et étudie les structures de corps et d’anneau. Dedekind définit les idéaux (déjà entrevus par Gauss) qui permettront de généraliser et reformuler les grands théorèmes d’arithmétique. L’algèbre linéaire se généralise en algèbre multilinéaire et algèbre tensorielle.
Au début du XXe siècle, sous l’impulsion de l’allemand Hilbert et du français Poincaré, les mathématiciens s’interrogent sur les fondements des mathématiques : logique et axiomatisation occupent le devant de la scène. Peano axiomatise l’arithmétique, puis les espaces vectoriels. La structure d’espace vectoriel et la structure d’algèbre sont approfondies par Artin en 1925, avec des corps de base autres que 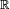 ou ou  et des opérateurs toujours plus abstraits. On doit aussi à Artin, considéré comme le père de l’algèbre contemporaine, des résultats fondamentaux sur les corps de nombres algébriques. Les corps non commutatifs amènent à définir la structure de module sur un anneau et la généralisation des résultats classiques sur les espaces vectoriels. et des opérateurs toujours plus abstraits. On doit aussi à Artin, considéré comme le père de l’algèbre contemporaine, des résultats fondamentaux sur les corps de nombres algébriques. Les corps non commutatifs amènent à définir la structure de module sur un anneau et la généralisation des résultats classiques sur les espaces vectoriels.
L’école française « Nicolas Bourbaki », emmenée par Weil, Cartan et Dieudonné, entreprend de réécrire l’ensemble des connaissances mathématiques sur une base axiomatique : ce travail gigantesque commence par la théorie des ensembles et l’algèbre dans le milieu du siècle, et confirme l’algèbre comme langage universel des mathématiques. Paradoxalement, alors que le nombre de publications suit une croissance exponentielle à travers le monde, alors qu’aucun mathématicien ne peut prétendre dominer qu’une toute petite partie des connaissances, les mathématiques n’ont jamais autant paru unifiées qu’aujourd’hui.
Notations européennes modernes
- Les symboles « + » et « – » apparaissent en 1489 dans l’ouvrage Arithmétique de John Widmann (Leipzig)
- Le signe « = » apparaît en 1557 chez Robert Recorde « parce que deux choses ne sauraient être plus égales que deux lignes parallèles« .
- Les signes « < » et « > » apparaissent en 1610 chez Thomas Harriot (1560-1621).
- William Oughtred (1574-1660) introduit le signe de la multiplication « x » dans son Clavis Mathematica (1631). Il introduit aussi les termes de sinus, cosinus et tangente.
- Le signe de la division « / » est utilisé par J. H. Rahn en 1659 et introduit en Angleterre par John Pell en 1668.
|

 Encyclopédie des métiers
Encyclopédie des métiers  Ajouter un métier
Ajouter un métier  Ajouter une vidéo métier
Ajouter une vidéo métier
 Encyclopédie des métiers
Encyclopédie des métiers  Ajouter un métier
Ajouter un métier  Ajouter une vidéo métier
Ajouter une vidéo métier